Difference Between a Batch and an Epoch in a Neural Network
For shorthand, the algorithm is often referred to as stochastic gradient descent regardless of the batch size. Given that very large datasets are often used to train deep learning neural networks, the batch size is rarely set to the size of the training dataset. The number of examples from the training dataset used in the estimate of the error gradient is called the batch size and is an important hyperparameter that influences the dynamics of the learning algorithm. Well, it’s up to us to define and decide when we are satisfied with an accuracy, or an error, that we get, calculated on the validation set. It could go on indefinitely, but it doesn’t matter much, because it’s close to it anyway, so the chosen values of parameters are okay, and lead to an error not far away from the one found at the minimum.In deep-learning era, it is not so much customary to have early stop. In deep-learning again you may have an over-fitted model if you train so much on the training data. To deal with this problem, another approaches are used for avoiding the problem. Adding noise to different parts of models, like drop out or somehow batch normalization with a moderated batch size, help these learning algorithms not to over-fit even after so many epochs. It is common to create line plots that show epochs along the x-axis as time and the error or skill of the model on the y-axis.
Stochastic Gradient Descent
However, it is well known that too large of a batch size will lead to poor generalization (although currently it’s not known why this is so). For convex functions that we are trying to optimize, there is an inherent tug-of-war between the benefits of smaller and bigger batch sizes.The blue points is the experiment conducted in the early regime where the model has been trained for 2 epochs. The green points is the late regime where the model has been trained for 30 epochs.
What should batch size?
The batch size is a number of samples processed before the model is updated. The number of epochs is the number of complete passes through the training dataset. The size of a batch must be more than or equal to one and less than or equal to the number of samples in the training dataset.Therefore, training with large batch sizes tends to move further away from the starting weights after seeing a fixed number of samples than training with smaller batch sizes. In other words, the relationship between batch size and the squared gradient norm is linear. Batch size is one of the most important hyperparameters to tune in modern deep learning systems. Practitioners often want to use a larger batch size to train their model as it allows computational speedups from the parallelism of GPUs.
Hypothesis: gradient competition
As expected, the gradient is larger early on during training (blue points are higher than green points). Contrary to our hypothesis, the mean gradient norm increases with batch size! We expected the gradients to be smaller for larger batch size due to competition amongst data samples. Instead what we find is that larger batch sizes make larger gradient steps than smaller batch sizes for the same number of samples seen. Note that the Euclidean norm can be interpreted as the Euclidean distance between the new set of weights and starting set of weights.
Effect of batch size on training dynamics
The reason for better generalization is vaguely attributed to the existence to “noise” in small batch size training. This “tug-and-pull” dynamic prevents the neural network from overfitting on the training set and hence performing badly on the test set. You can think of a for-loop over the number of epochs where each loop proceeds over the training dataset.During training by stochastic gradient descent with momentum (SGDM), the algorithm groups the full dataset into disjoint mini-batches. Next, we can create a function to fit a model on the problem with a given batch size and plot the learning curves of classification accuracy on the train and test datasets. Namely, that the model rapidly learns the problem as compared to batch gradient descent, leaping up to about 80% accuracy in about 25 epochs rather than the 100 epochs seen when using batch gradient descent.However, by increasing the learning rate to 0.1, we take bigger steps and can reach the solutions that are farther away. Interestingly, in the previous experiment we showed that larger batch sizes move further after seeing the same number of samples. The picture is much more nuanced in non-convex optimization, which nowadays in deep learning refers to any neural network model. It has been empirically observed that smaller batch sizes not only has faster training dynamics but also generalization to the test dataset versus larger batch sizes. But this statement has its limits; we know a batch size of 1 usually works quite poorly.
Develop Deep Learning Projects with Python!
- In this example, we will use “batch gradient descent“, meaning that the batch size will be set to the size of the training dataset.
- A batch size of 32 means that 32 samples from the training dataset will be used to estimate the error gradient before the model weights are updated.
- The model will be fit for 200 training epochs and the test dataset will be used as the validation set in order to monitor the performance of the model on a holdout set during training.

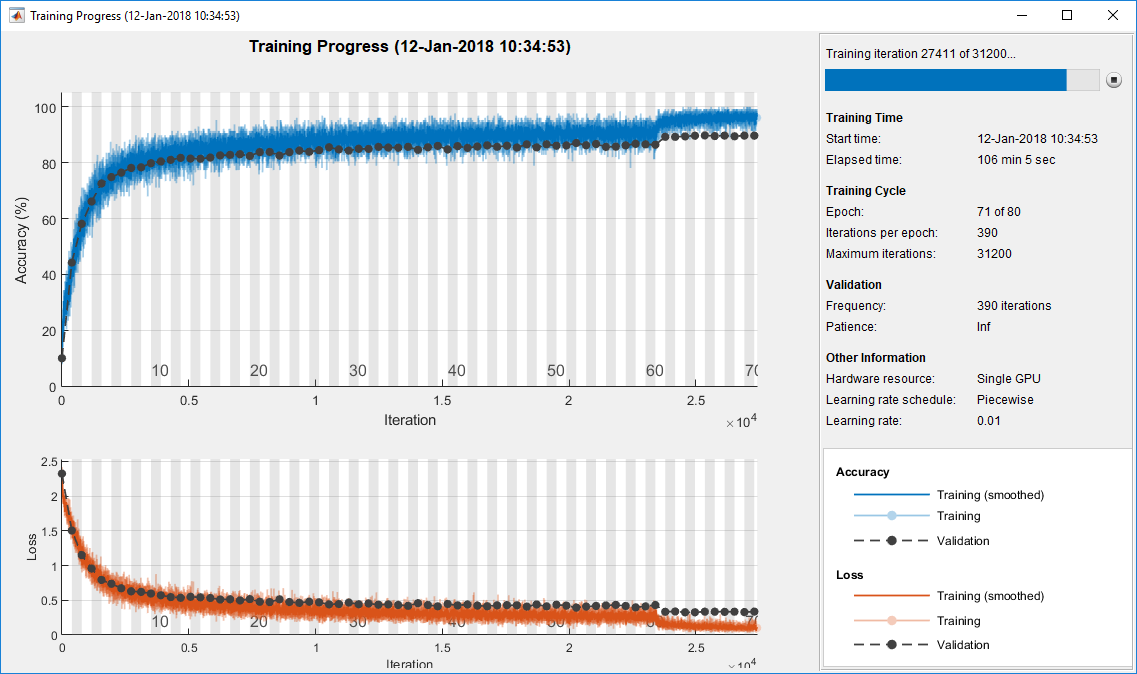
On the one extreme, using a batch equal to the entire dataset guarantees convergence to the global optima of the objective function. However, this is at the cost of slower, empirical convergence to that optima. On the other hand, using smaller batch sizes have been empirically shown to have faster convergence to “good” solutions. It will bounce around the global optima, staying outside some ϵ-ball of the optima where ϵ depends on the ratio of the batch size to the dataset size. The mini-batch accuracy reported during training corresponds to the accuracy of the particular mini-batch at the given iteration.These plots can help to diagnose whether the model has over learned, under learned, or is suitably fit to the training dataset. One epoch means that each sample in the training dataset has had an opportunity to update the internal model parameters.In this example, we will use “batch gradient descent“, meaning that the batch size will be set to the size of the training dataset. The model will be fit for 200 training epochs and the test dataset will be used as the validation set in order to monitor the performance of the model on a holdout set during training. A batch size of 32 means that 32 samples from the training dataset will be used to estimate the error gradient before the model weights are updated.
What Is the Difference Between Batch and Epoch?
One training epoch means that the learning algorithm has made one pass through the training dataset, where examples were separated into randomly selected “batch size” groups. When all training samples are used to create one batch, the learning algorithm is called batch gradient descent.
What is a batch size?
Batch size (machine learning) Batch size is a term used in machine learning and refers to the number of training examples utilized in one iteration. The batch size can be one of three options: batch mode: where the batch size is equal to the total dataset thus making the iteration and epoch values equivalent.
Batch size
When the batch is the size of one sample, the learning algorithm is called stochastic gradient descent. When the batch size is more than one sample and less than the size of the training dataset, the learning algorithm is called mini-batch gradient descent.It is generally accepted that there is some “sweet spot” for batch size between 1 and the entire training dataset that will provide the best generalization. This “sweet spot” usually depends on the dataset and the model at question.For example, as above, an epoch that has one batch is called the batch gradient descent learning algorithm. For Deep Learning training problems the “learning” part is really minimizing some cost(loss) function by optimizing the parameters (weights) of a neural network model. This is a formidable task since there can be millions of parameters to optimize. The loss function that is being minimized includes a sum over all of the training data. It is typical to do some optimization method that is a variation of stochastic gradient descent over small batches of the input training data.The optimization is done over these batches until all of the data has been covered. One complete cycle through all of the training data is usually called an “epoch”. Optimization is iterated for some number of epochs until the loss function is minimized and accuracy of the models predictions have reached an acceptable accuracy (or it has just stopped improving). The y-axis shows the average Euclidean norm of gradient tensors across 1000 trials. The error bars indicate the variance of the Euclidean norm across 1000 trials.
What is batch size in neural network?
We could have stopped training at epoch 50 instead of epoch 200 due to the faster training. The example below uses the default batch size of 32 for the batch_size argument, which is more than 1 for stochastic gradient descent and less that the size of your training dataset for batch gradient descent. The best solutions seem to be about ~6 distance away from the initial weights and using a batch size of 1024 we simply cannot reach that distance. This is because in most implementations the loss and hence the gradient is averaged over the batch. This means for a fixed number of training epochs, larger batch sizes take fewer steps.
