Points, Lines and CurvesLikewise, the distance from a point to a curve is measured by a line segment that is perpendicular to a tangent line to the curve at the nearest point on the curve. The distance from a point to a line is the distance to the nearest point on that line.
Euclidean geometry
What is a point in math definition?
A point in geometry is a location. It has no size i.e. no width, no length and no depth. A point is shown by a dot. A line is defined as a line of points that extends infinitely in two directions. It has one dimension, length.

Two distinct lines perpendicular to the same plane must be parallel to each other.Conversely, if one line is perpendicular to a second line, it is also perpendicular to any line parallel to that second line. The segment AB is perpendicular to the segment CD because the two angles it creates (indicated in orange and blue) are each 90 degrees. The segment AB can be called the perpendicular from A to the segment CD, using “perpendicular” as a noun.
An introduction to geometry
Euclid set forth the first great landmark of mathematical thought, an axiomatic treatment of geometry. He selected a small core of undefined terms (called common notions) and postulates (or axioms) which he then used to prove various geometrical statements.A plane is the two-dimensional analogue of a point (zero dimensions), a line (one dimension) and three-dimensional space. Planes can arise as subspaces of some higher-dimensional space, as with a room’s walls extended infinitely far, or they may enjoy an independent existence in their own right, as in the setting of Euclidean geometry. More specifically, in Euclidean geometry, a point is a primitive notion upon which the geometry is built, meaning that a point cannot be defined in terms of previously defined objects. That is, a point is defined only by some properties, called axioms, that it must satisfy. In particular, the geometric points do not have any length, area, volume or any other dimensional attribute.
What is a Point in Math? – Definition & Example
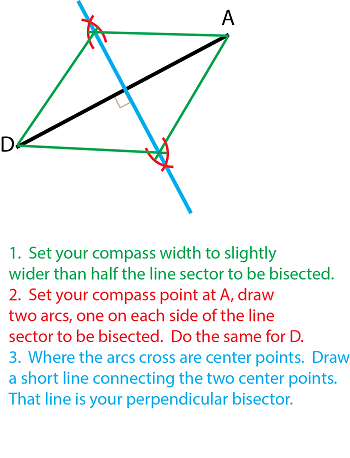
In elementary geometry, the property of being perpendicular (perpendicularity) is the relationship between two lines which meet at a right angle (90 degrees). Points are important parts of math, and they can be used to label shapes and angles on a plane. In modern mathematics, a point refers usually to an element of some set called a space. Up to three lines in three-dimensional space can be pairwise perpendicular, as exemplified by the x, y, and z axes of a three-dimensional Cartesian coordinate system.This definition depends on the definition of perpendicularity between lines. A line is said to be perpendicular to another line if the two lines intersect at a right angle. Perpendicularity can be shown to be symmetric, meaning if a first line is perpendicular to a second line, then the second line is also perpendicular to the first. For this reason, we may speak of two lines as being perpendicular (to each other) without specifying an order. When working exclusively in two-dimensional Euclidean space, the definite article is used, so, the plane refers to the whole space.The perpendicular bisectors of the sides also play a prominent role in triangle geometry. Thales’ theorem states that two lines both through the same point on a circle but going through opposite endpoints of a diameter are perpendicular. This is equivalent to saying that any diameter of a circle subtends a right angle at any point on the circle, except the two endpoints of the diameter. A line segment through a circle’s center bisecting a chord is perpendicular to the chord.
Point-normal form and general form of the equation of a plane
- Although the plane in its modern sense is not directly given a definition anywhere in the Elements, it may be thought of as part of the common notions.
- Euclid set forth the first great landmark of mathematical thought, an axiomatic treatment of geometry.
- He selected a small core of undefined terms (called common notions) and postulates (or axioms) which he then used to prove various geometrical statements.
Many fundamental tasks in mathematics, geometry, trigonometry, graph theory, and graphing are performed in a two-dimensional space, or, in other words, in the plane. Points can be used to name angles and shapes, such as rectangle ABCD or line segment YZ.The point B is called the foot of the perpendicular from A to segment CD, or simply, the foot of A on CD. In mathematics, a plane is a flat, two-dimensional surface that extends infinitely far.
What is the point meaning?
“The point” of something is the reason for doing it. But this word is often used in the negative sense: “what’s the point?”, “there’s no point”, “I don’t see the point”, etc.
Intersecting Lines
Similar constructions exist that define the plane, line segment and other related concepts. A line segment consisting of only a single point is called a degenerate line segment. To prove that the PQ is perpendicular to AB, use the SSS congruence theorem for ‘ and QPB’ to conclude that angles OPA’ and OPB’ are equal. Then use the SAS congruence theorem for triangles OPA’ and OPB’ to conclude that angles POA and POB are equal.
Plane (geometry)
Harcourt’s theorem concerns the relationship of line segments through a vertex and perpendicular to any line tangent to the triangle’s incircle. The Droz-Farny line theorem concerns a property of two perpendicular lines intersecting at a triangle’s orthocenter. The Euler line of an isosceles triangle is perpendicular to the triangle’s base. The altitudes of a triangle are perpendicular to their respective bases.
What is a preposition?
Although the plane in its modern sense is not directly given a definition anywhere in the Elements, it may be thought of as part of the common notions. In this way the Euclidean plane is not quite the same as the Cartesian plane. If two lines (a and b) are both perpendicular to a third line (c), all of the angles formed along the third line are right angles. Therefore, in Euclidean geometry, any two lines that are both perpendicular to a third line are parallel to each other, because of the parallel postulate.That is the point at which a segment from it to the given point is perpendicular to the line. In addition, the Euclidean geometry (which has zero curvature everywhere) is not the only geometry that the plane may have. The plane may be given a spherical geometry by using the stereographic projection. This can be thought of as placing a sphere on the plane (just like a ball on the floor), removing the top point, and projecting the sphere onto the plane from this point). This is one of the projections that may be used in making a flat map of part of the Earth’s surface.A common interpretation is that the concept of a point is meant to capture the notion of a unique location in Euclidean space. Two planes in space are said to be perpendicular if the dihedral angle at which they meet is a right angle (90 degrees). A line is said to be perpendicular to a plane if it is perpendicular to every line in the plane that it intersects.